近日,北京大学工学院教授王建祥课题组揭示了一系列格栅结构的拓扑动力学性质,该项研究以“The topological dynamics of continuum lattice grid structures”为题在线发表于国际固体力学旗舰期刊Journal of the Mechanics and Physics of Solids。
力学系统的拓扑模态由于对缺陷免疫和能量分布可调的性质而被广泛关注,其拓扑性质的理论研究通常基于经典的离散模型——弹簧质量模型。在自然界和工业应用中,连续介质系统更为常见,其拓扑力学性质更为丰富,且具有重要的理论及实际应用价值。但是,理论求解连续介质系统的拓扑性质具备相当的复杂性,研究者们主要通过设计惯性或刚度调制的超材料并且使用数值计算的方法来近似分析其拓扑性质。因此,构建一类具有精确解析解的连续拓扑系统,对深入理解和应用连续体中的各种拓扑相至关重要。自然界和工程领域中普遍存在的均质弹性梁所构成的格栅结构(例如动物和植物体中的多孔结构、桥梁和建筑物框架、人工设计的微纳米多孔材料等)是一类典型的连续介质系统,其拓扑动力学性质还未被探究和精确表征。
该项研究首次揭示了多种格栅结构的拓扑动力学性质。从具有周期性排列简支支承的连续梁系统(图1)开始,研究团队提出了一种创新的方法来获取梁的拓扑振动模式。与目前材料特性受空间周期调制的拓扑结构不同,这种梁结构的材料性质是均匀的,因此更易于生产和应用。该方法可以推广应用于桥式刚架【图2(a)】、正方形格栅刚架【图2(b)】、Kagome格栅刚架【图2(c)】、支承在弹性基础或弹性支座上的连续梁结构以及均质的板结构,精确计算它们的拓扑边态或高阶拓扑角态。同时,该项研究构建了一套简洁的理论框架,发现了一个这类结构拓扑模态的存在性定理,用来解析且精确地计算这些格栅结构中无穷多个拓扑模态的频率,并给出多次拓扑相变的清晰判据。揭示格栅结构的拓扑性质不仅为设计具备特定拓扑力学性质的连续体结构提供了新颖的视角,并在连续体系统拓扑动力学的精确理论分析方面取得了重要进展。此外,这些研究成果在结构的波动与振动控制、健康监测与安全性分析,以及基于物质变形和运动的能量收集技术等多个领域具有应用前景。

图1 具备拓扑性质的连续梁系统。(a)拓扑连续梁结构。(b)连续梁系统中的一对频率简并的拓扑边态,能量局域化在系统的边界上
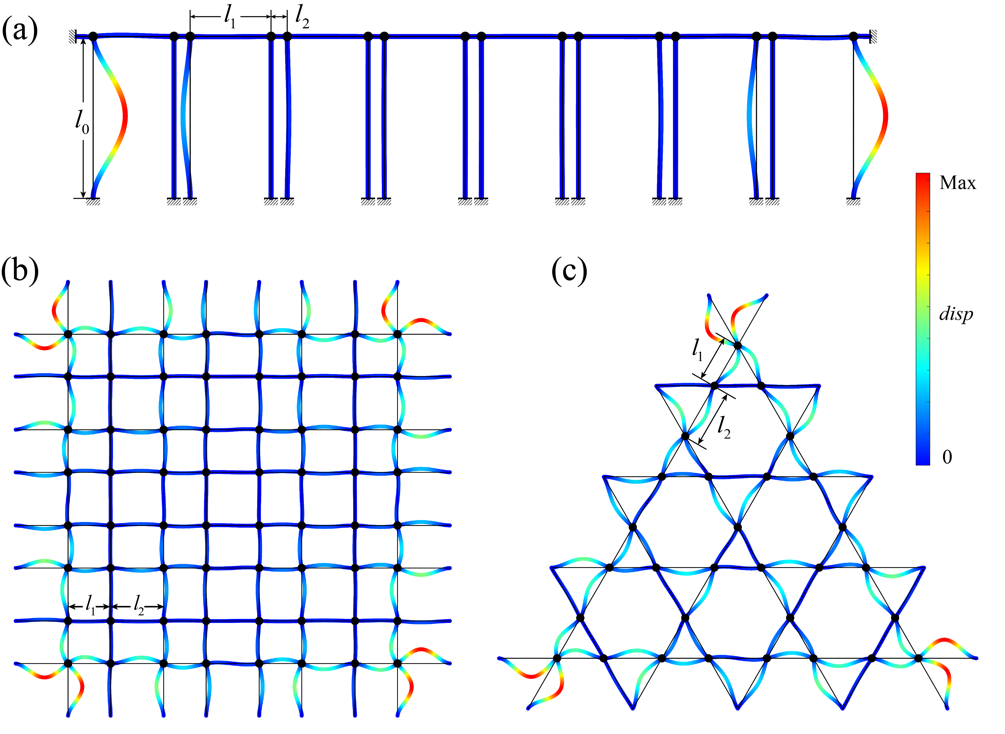
图2 具备拓扑性质的格栅结构。(a)桥式刚架结构。(b)正方形格栅刚架结构。(c)Kagome格栅刚架结构。能量局域化在系统的边界或角点上
北京大学工学院博士研究生孙艺萌为论文的第一作者,博士研究生邢家诚为论文的第二作者,论文合作者还包括北京航空航天大学教授邵丽华,王建祥为通讯作者。论文工作得到国家自然科学基金以及北京自然科学基金的资助。







