清华新闻网9月24日电 近日,清华大学丘成桐数学科学中心教授刘正伟,博士生邵钰菓、魏付川,北京雁栖湖应用数学研究院助理研究员程嵩提出了一种计算含噪声量子线路期望值的高效方法——泡利基上的算符反向传播(Observable's Back-propagation on Pauli Paths,OBPPP),这一变分量子算法在精度和速度上均优于量子硬件,并可应用于更广泛类别的量子电路中。
目前,量子计算正处于所谓的“含噪声中等规模量子硬件时代(NISQ Era)”。变分量子算法凭借其对量子硬件更低的要求,有望率先实现可应用且有意义的量子算法,因而在组合优化、量子化学、材料计算乃至机器学习等领域都备受关注。但变分量子算法的研究仍面临着诸多难题,如线路噪声带来的退相干、表达能力的局限、可训练性的丧失等。事实上,找到相对经典且真正具备量子优势的变分量子算法,依旧是一个科学界反复讨论又难以解决的开放问题。一个同样重要的反问题是:什么类型的变分量子算法是容易被经典模拟的?
数学中心量子对称团队从理论上证明了一大类常见的变分量子算法,其架构均不具有量子优势。基于这一理论,团队创造性地构建了一个切实可算的多项式复杂度的经典算法——OBPPP,并与上述变分量子算法进行对比,获得了喜人的结果。
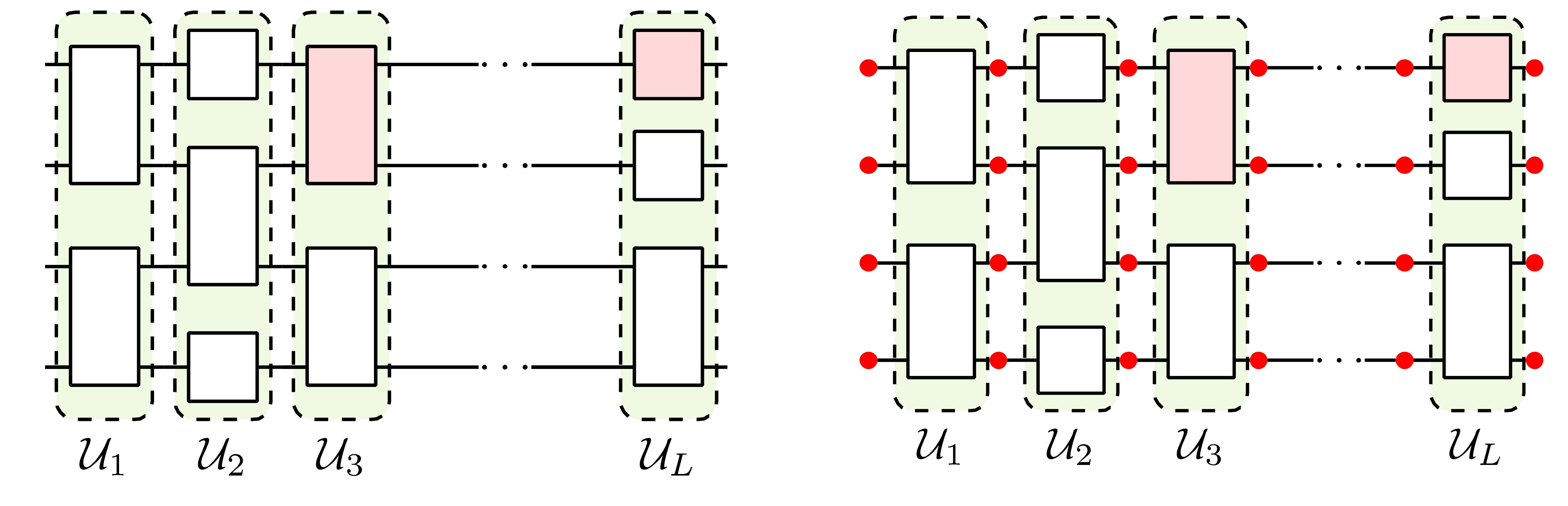
左:无噪声量子线路示意图 右:含噪声量子线路示意图
该工作考察了由Clifford门与任意比特单参数Pauli旋转门共同组成的量子线路(上图分别对应白色和粉色方块表示),囊括了当前大部分变分量子算法的线路架构。同时考虑线路中存在独立的单比特Pauli型噪声通道,这一噪声模型包括了实验中最常见的去极化噪声(depolarizing)和退相位噪声(dephasing)等。研究团队认为,同样的方法也可以很容易地推广至更普遍的单比特噪声,比如保单位噪声(unital noise)。
对于上述常见的变分量子线路架构,研究人员发现在Pauli基上将整个线路进行傅里叶展开,观测算符在线路上的期望值,表达为在Pauli基上的路径积分,可以大幅度提高现有经典算法对于变分量子算法的模拟速度。这一方法有两个显著的好处,其一,由Clifford门与任意比特单参数Pauli旋转门组成的量子线路在此展开下性质良好,展开的项数往往少于传统算法(例如张量网络方法中的求和项,状态矢量state vector方法中的计算基项);其二,在Pauli型噪声参与的情况下,大量路径的贡献受到压制且压制系数具有清楚的表达式:
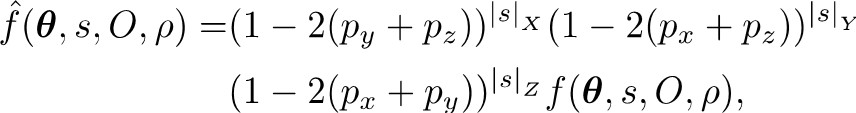
这保证了有限数值精度的前提下,能够做到算法复杂度仅随量子线路深度与量子比特数多项式增长。
研究人员在理论上证明了这类含噪声量子线路算符期望的经典可模拟性。他们发现全体Pauli型噪声可以分为两种情形,保持一个固定的截断误差,各自证明了两种情形下经典模拟的时间复杂度为:
情形一: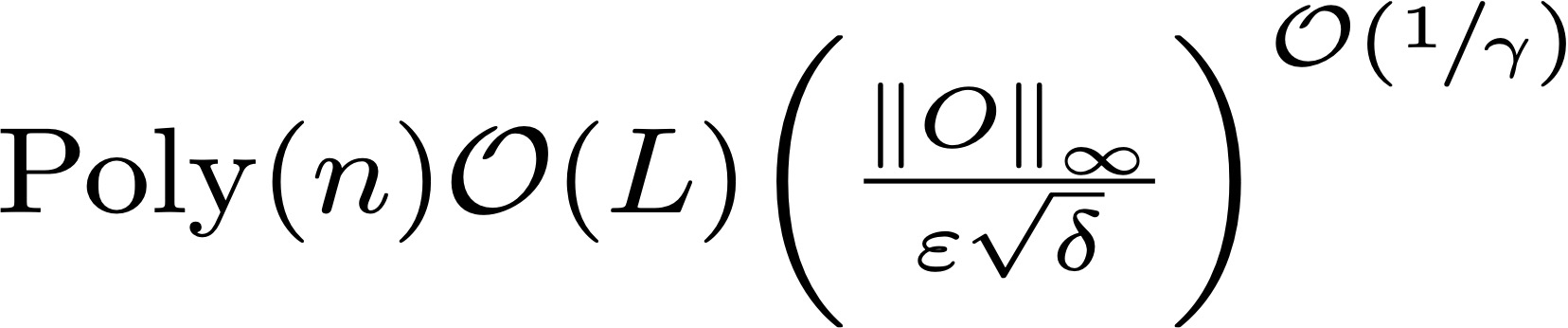
情形二: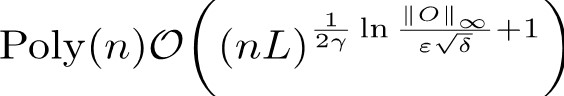
其中n为比特数,L为深度,Epsilon为数值误差,Gamma为噪声率。事实上,在常数非零噪声率下,OBPPP的时间和空间复杂度与量子比特数n和电路深度L均呈多项式关系。在一般的线路中通常为指数关系。
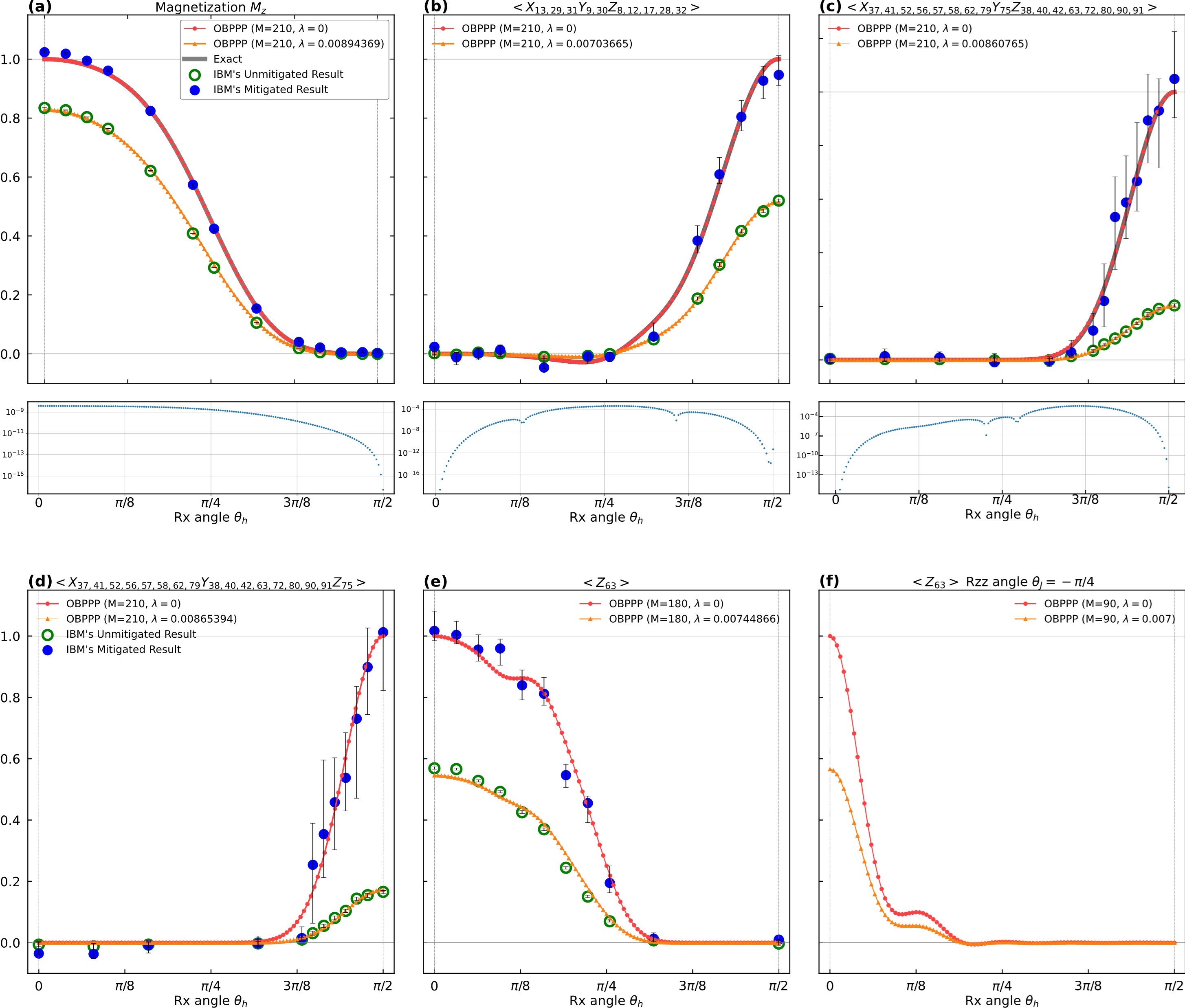
模拟结果与IBM Eagle量子处理器的实验结果高度吻合
研究人员成功地对IBM的Eagle量子处理器的算法进行了经典模拟,运行时间比量子硬件更短,同时实现了更准确的期望值。以模拟IBM算法实验为例,量子比特数为127,线路深度为80,OBPPP得到每张图的计算时间均小于5分钟(基于2张Xeon6330 CPU的结果)。此外,对不同的噪声率,根据路径压制因子,从而很容易地推出对应算符期望值,与未修正的原始实验数据直接对比,表现出与实验结果很强的一致性。
研究针对含单比特Pauli型噪声的变分量子线路,考虑线路由Clifford门与任意比特单参数Pauli旋转门组成。研究人员发现,OBPPP能够实现此线路下算符期望值的高效近似,并保证有界的截断误差。研究团队在理论上证明了存在常数非零噪声率时,OBPPP的时间和空间复杂度与量子比特数n和电路深度L均呈多项式关系。数值上,通过对IBM 127量子比特Eagle处理器的经典模拟,验证了该方法在精度和运行速度上均优于量子硬件,能够准确模拟还原噪声影响下的实验结果。此外,该工作还细致地揭示了噪声与经典可模拟性的关系,展示了该方法在更广泛类别的量子电路中的适用性。
9月18日,相关研究成果以“模拟含噪声变分量子算法:一种多项式途径”(Simulating Noisy Variational Quantum Algorithms: A Polynomial Approach)为题,发表于《物理评论快报》(Physical Review Letters)。
清华大学丘成桐数学科学中心与北京雁栖湖应用数学研究院共同完成这项工作。论文第一作者为数学中心2020级博士生邵钰菓。刘正伟、程嵩为论文通讯作者。数学中心2021级博士生魏付川参与合作。









